
Hiding a Sentence in a Compact Grid of Letters
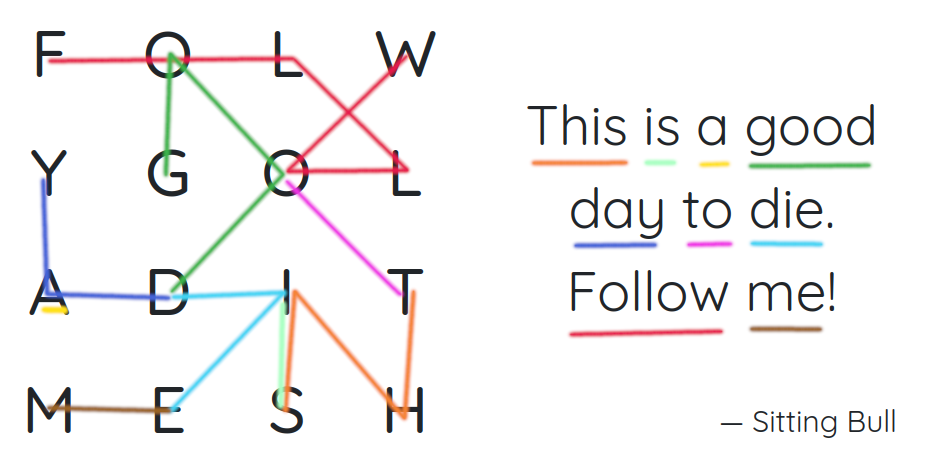
When playing Gridogram, your goal is to trace words in a letter grid to find the hidden quote. This page is about what goes on behind the scenes: starting with a quote, how do we create its letter grid?
All the words in the following quote can fit in a 4x4 grid.
Space is to place as eternity is to time.
Try it yourself: set letters in the grid so that all words in the above quote are underlined. One cell can even be left blank, there are multiple solutions. The starting letters are part of a possible solution, but you can change them.
The first Gridograms were created with pencil and paper, trial and error, using heuristics you may have discovered by trying to fill the grid above. It can be a fun and frustrating challenge, a little like sudoku.
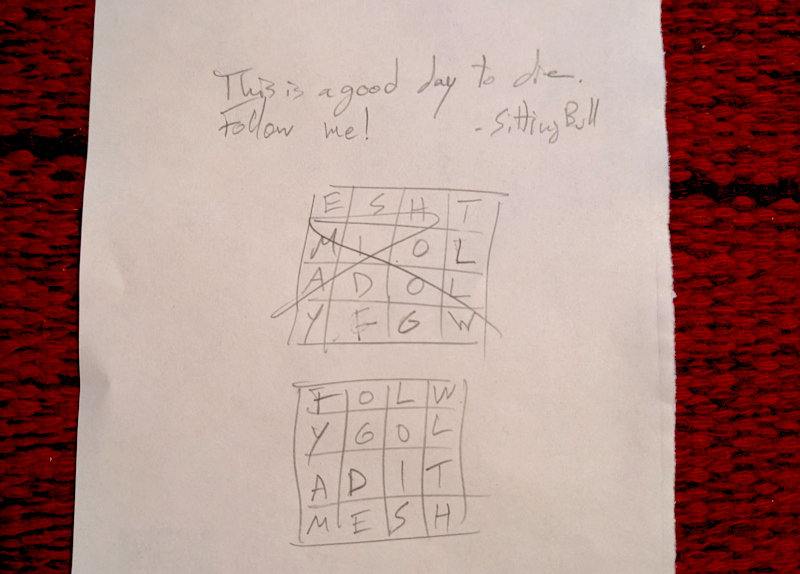
But how did we know that a 4x4 grid was the right size for the quote?
Take the letters in “Space is to place as eternity is to time”, noting that T and E are needed twice to spell “eternity”:
ACEEILMNOPRSTTY
That’s 15 letters, and for this quote we indeed need 15 grid cells. We use 4x4 rather than 5x3 to keep Gridograms near square, as 𝑛x𝑛 or 𝑛x𝑛−1.
Often, however, this counting exercise only gives us a lower bound, not the exact number of cells needed. Let’s try another quote:
Thank heavens, the sun has gone in, and I don’t have to go out and enjoy it.
Letters used:
ADEEGHIJKNOSTUVY
That’s 16 letters, so another 4x4 grid? Nope, that won’t be big enough to include all the words. Can you figure out a reason why, looking at how many different letters are next to the letter N in the quote? (I’ll come back to this.)
Why estimate grid size?
Grid size is one of the key criteria for deciding whether a quote can feature as a Gridogram. The majority of Gridograms are 4x4 or 5x4. An occasional 5x5 makes the cut, but can take players significantly longer to solve — sometimes too long for what’s meant to be a fun casual daily game.
Large grids can also take significant amounts of time to find. We want to fit multiple words on paths in a grid, and a 4x4 grid has 12,029,640 different paths. A 5x5 grid has 115,066,382,913 paths. Yes, I have left an algorithm running for days trying to find a grid! But I have not yet tried a quote that needs a 6x6 grid with 9,913,814,758,253,424 paths. [1]
So why can’t “Thank heavens, the sun has gone in, and I don’t have to go out and enjoy it” fit in a 4x4 grid?
Cells in a grid corner connect with 3 others. Cells on the side connect with 5. Cells away from the sides have the most connections: 8.
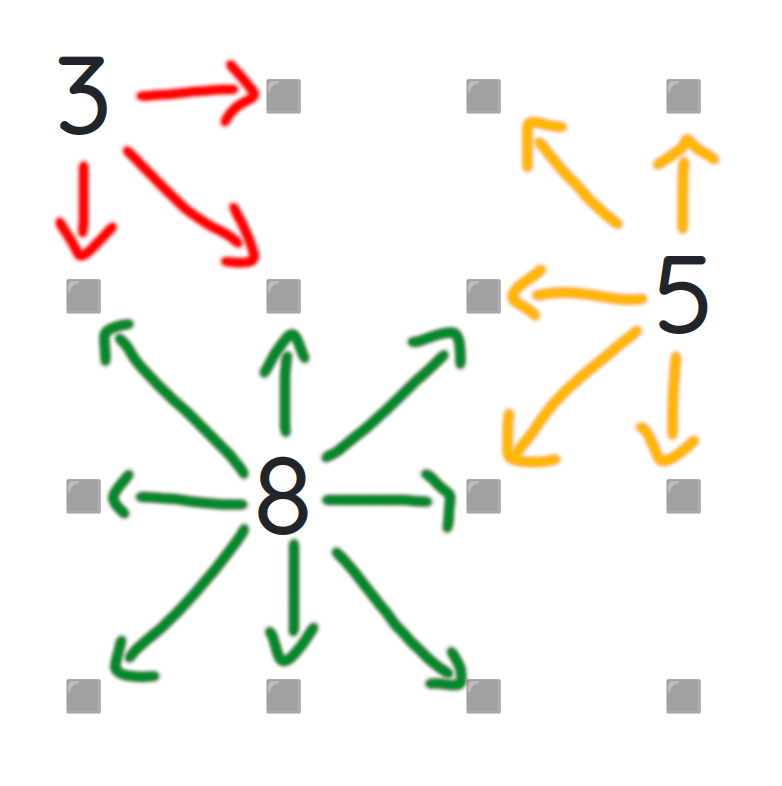
The letter N in the quote is very friendly: it wants to be next to A, D, E, I, J, K, O, S, and U. That’s 9 different letters, more adjacencies than one grid cell can have!
So the grid will need more than one N. Updating the letter list to ADEEGHIJKNNOSTUVY gives us a new lower bound of 17 letters. The quote does indeed fit in a 5x4 grid, you can try to create one below (3 cells can be left blank).
Thank heavens, the sun has gone in, and I don’t have to go out and enjoy it.
How can we programmatically take account of cases like this quote, to better estimate grid size? With undirected graphs!
We can generate an undirected graph for the quote, so that each word can be made by starting at its first letter and tracing a path through connected letters, without visiting the same letter twice. Such a graph looks like this, with the letters for “thank” highlighted as an example:
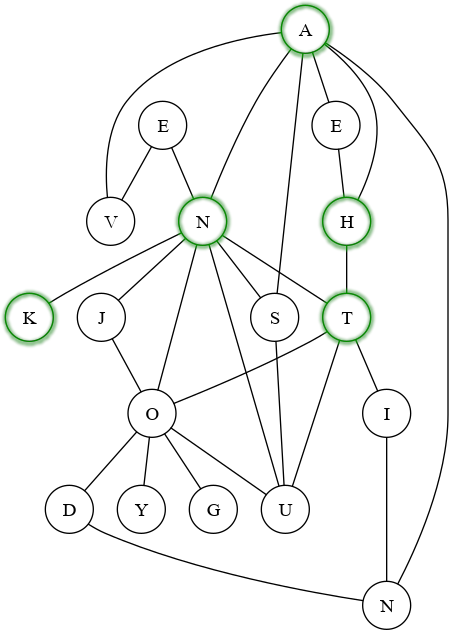
Because there are multiple nodes for the same letter, there are different ways to build the graph to include all the words. Investigating the space of all potential graphs is too computationally expensive, but we can guide the graph building process. For example, given “heaven” with two E nodes is in the graph, there are two options to connect “heaven” with the E in “the”, but we naturally select the E already connected to an H.
Given the goal is to estimate Gridogram size, we apply certain constraints when building a graph to exclude those that cannot be mapped to a grid. One constraint is that no node (letter) can have more than 8 edges, the most adjacencies one letter can have in a grid. This is why we end up with two Ns above, one with 8 edges and one with 3 edges, even though no individual word requires more than one N.
Let’s look at a different and non-obvious constraint, using a new quote and a new graph. The problematic letters are in red, can you see why they and their intermediate connections cannot be mapped to a grid?
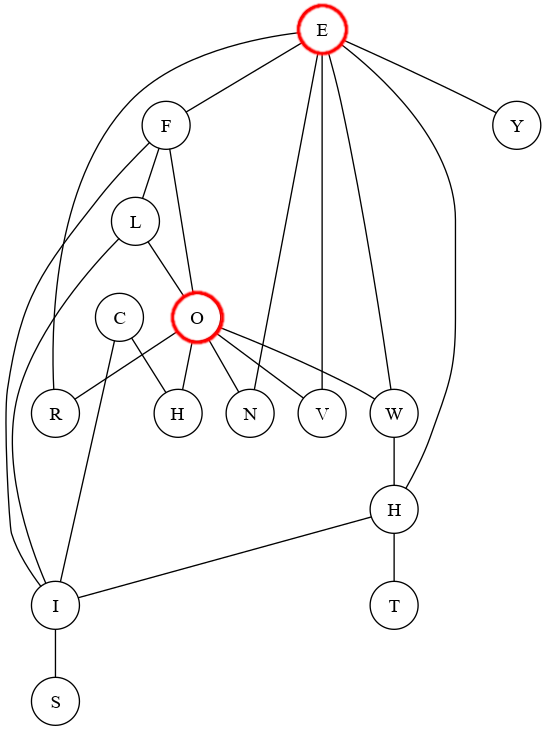
Look at the letters E and O in a grid:

It’s possible to trace 4 different paths with one cell between E and O: one path through each of the numbers. Each path can be reversed, that does not matter. What does matter is that 4 is the maximum, there is no way to place E and O differently to allow more than 4 paths with exactly one letter between them. [2]
The graph for the Victor Hugo quote has 5 letters immediately between E and O — EFO, ERO, ENO, EVO, and EWO — so this subgraph cannot be mapped to a grid. When building a graph, we actually prevent such subgraphs being created: instead we must add another node, which in this case could be any of E, F, O, R, N, V, or W.
Once a graph is generated satisfying all constraints, this gives an improved lower bound estimate on the number of letters needed: it still doesn’t give us the Gridogram, or even the exact letter count. It is still possible that the generated graph is not isomorphic to a subgraph of the grid graph, and I don’t know if further improvements to the estimate are possible with this approach. [3]
Estimating grid size with a graph is a quick way to rule out quotes that will not fit in a Gridogram. For remaining quotes that do have a chance of fitting, the computationally expensive brute force search for a corresponding letter grid then begins.
[1]: The On-Line Encyclopedia of Integer Sequences (A236690). Even getting a count for how many paths exist is not trivial. I wrote a naive Fortran program (new language for me, wanted to try it) to exhaustively count the paths for 2x2 (64), 3x3 (10,305), and 4x4 (12,029,640) grids. 5x5 was taking some time to compute, fortunately pasting the path counts for smaller grids in Google led me to the OEIS.
[2]: Thank you to Joseph Loughney at the University of St Andrews for pointing out this constraint.
[3]: Thank you to Matthew Spam on the Mathematics Stack Exchange for pointing me to the Subgraph isomorphism problem. Thank you to Ciaran McCreesh at the University of Glasgow help understanding the functionality of the Glasgow Subgraph Solver, and for sharing my letter grid problem with colleagues. The Glasgow Subgraph Solver can be used to determine whether a graph is a subgraph of the grid graph, and provide a mapping if it is. But when the graph is not a subgraph of the grid graph it’s not possible to see what changes are needed to make it one — not a fault of the subgraph solver, but would have been useful for making Gridograms!